حساب المساحات والحجوم
تعتبر العمليات الخاصة بحساب المساحات سواء من الخرائط او من الطبيعة من العمليات الاساسية في عمل المساح وتتوقف دقة حساب المساحة علي دقة القياس وعلي الرغم من ان ادق الطرق لحساب المساحات هو القياس المباشر من الطبيعة لآطوال وزوايا الشكل المطلوب ايجاد مساحته الا ان ادق الطرق لحساب المساحات هو القياس المباشر من الطبيعة لآطوال وزوايا الشكل المطلوب ايجاد مساحته الا ان القياس من الخريطة هو الاكثر شيوعا عند حساب المساحات وذلك لسهولة القياس من الخريطة رغم ماقد يكون بها من اخطاء في الرسم.
حساب مساحة الارض
وقد تكون قطع الاراضي او الاشكال المطلوب تعيين مساحتها علي هيئة اشكال هندسية منتظمة او غير منتظمة الشكل فالاشكال المنتظمة هي الاشكال البسيطة مثل المثلث والاشكال الرباعية بأنواعها مثل المربع والمستطيل ومتوازي الاضلاع والمعين وشبه المنحرف اما الاشكال غير المنتظمة فهي الاشكال ذات الحدود المتعددة والمتعرجة والتي لايمكن وصفها بشكل هندسي بسيط او منتظم وفي هذه الوحدة سنعرض لطرق حساب مساحة كل منها.
حساب مساحة الاشكال الغير المنتظمة
مساحة اشكال يمكن تقسيمها الي مثلثات تتوقف طريقة حساب المساحة للمثلثات علي المعلومات والارصاد المتاحة في الشكل وذلك باختيار احد رؤؤس المضلع وتوصيل هذا الرأس بكل رؤؤس المضلع ثم بقياس جميع الاضلاع يتم حساب مساحة كل مثلث علي حدة كما سبق شرح ذلك في مادة الحساب الفني ثم يتم تجميع مساحات المثلثات المكونة لهذا الشكل فينتج لدينا المساحة الكلية للشكل.
مثال :
الشكل التالي يوضح قطعة ارض محددة بمضلع أ ب ج د ه غير منتظم وكانت اطوال اضلاعة 15,21,17,22,20 متر علي الترتيب ,وزاوية أ قائمة , وزاوية ب د ه = 70ْ , وتم رسم الخط ب د وقيس طوله فكان = 25,6 متر . احسب مساحة قطعة الارض المحددة بهذا المضلع
الحل :
حيث ان قطعة الارض محددة بمضلع غير منتظم الشكل , لذلك يتم تقسيمها الي مثلثات , نحسب مساحة كل منها علي حدة ,ثم نجمع هذه المساحات لنحصل علي المساحة الكلية لقطعة الارض :
القاعدة × الارتفاع
1- مساحة المثلث أ ب ه = _________________________
2
20 ×15
مساحة المثلث أ ب ه = ______________________ = 150 م2
2
1
2 - مساحة المثلث ب د ه = ____________ × ب د × د ه × جا ب 3 ه
2
1
مساحة المثلث ب د ه = _____________ × 25,60 ×22× جا70 = 264,617 م2
2
21 +17 +25,6
مساحة المثلث ب ج د : اولا نحسب قيمة ح = ______________________ = 31,80 متر
2
____________________________
- مساحة المثلث ب ج د =/ا ح(ح - ب ج)(ح - ج د ) (ح - د ب )
_______________________________
مساحة المثلث ب ج د = /ا 31,8 ×10,8 ×14,8 ×6,2
مساحة المثلث ب ج د = 177,522 م2
اذا مساحة الشكل أ ب ج د ه =
مساحة المثلث أ ب ه + مساحة المثلث ب د ه + مساحة المثلث ب ج د
اذا مساحة الشكل أ ب ج د ه = 150 + 264,617+177,522
=592,139 م2
وهذه الطريقة شائعة الاستعمال وهي من الطرق التي تسهل عملية حساب المساحات للأراضي ولابد للقارئ والباحث ان يكون علي علم كافي بحساب المساحات الهندسية
مثال :
قطعة ارض علي شكل معين تم قياس طول قطريها فكانا علي الترتيب 30,20 متر , احسب مساحة قطعة الارض
الحل :
بما ان : مساحة المعين = 1/2 حاصل ضرب القطرين
اذا : م = 1/2 ×30,20 ×25,13 = 379,463 م2
مثال :
قطعة ارض علي شكل شبه منحرف - تم قياس قاعدتيه المتوازيتين فكانتا علي الترتيب 12 متر , وتم قياس المسافة العمودية بين القاعدتين المتوازيتين فكانت 9 متر .
فاحسب مساحة شبه المنحرف أ ب ج د
الحل :
مساحة الاشكال غير المنتظمة بتقسيمها الي اشباه منحرفات
اذا كانت قطعة الارض المطلوب ايجاد مساحتها احد حدودها متعرج والحد الاخر مستقيم او كلا من حديها متعرج الشكل فأن قطعة الارض تقسم الي مجموعة من اشباه المنحرفات ونحسب مساحة كل شبة منحرف علي حدة , ثم نجمع مساحات اشباه المنحرفات فنحصل علي المساحة الكلية لقطعة الارض ,
مثال :
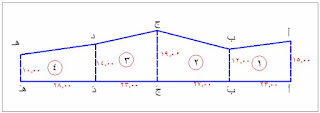
قطعة ارض كما بالشكل - احد حدودها متعرج الشكل والحد الاخر مستقيم اسقطت اعمدة من النقاط أ ,ب , ج ,د , ه علي الحد المستقيم وكانت اطوالها كما يلي :
أأَ = 15,00 م , ب بَ = 12,00 م , ج جَ= 19,00 م ,د دَ = 14,00 م , ه هَ = 10,00 م وكانت المسافات بين الاعمدة علي خط القاعدة كما يلي
أََ بَ = 23,00 م , بَ جَ = 27,00 م , جَ دَ = 23,00 م , دَ هَ = 28,00 م احسب مساحة هذه القطعة
الحل :
15,00 +12,00
مساحة شبة المنحرف رقم 1 = ______________________ × 23,00 = 310,50 م2
2
12,00 +19,00
مساحة شبة المنحرف رقم 2 = _______________________ × 27,00 = 418,50 م2
2
19,00 +14,00
مساحة شبه المنحرف رقم 3 = _______________________ ×23,00 =379’50 م2
2
14,00 +10,00
مساحة شبة المنحرف رقم 4 = _______________________×28,00 =336,00 م2
2
المساحة الكلية لقطعة الارض = 310,50 + 418,50 +379,50 336,00 = 1444,50 م2