المساحة 

المساحة

1-حساب وتقدير المساحة

أما من الخرائط أو من الطبيعة  مع الاخذ بعين الاعتبار أن المساحة التي تحسب عن طريق المسقط الافقي وليست عن طريق المساحة الحقيقية أي أنه دائما نأخذ المسافات الافقية وليست المائلة  وتقدير المساحة الطبيعية المساحة الخرائط وطرق إيجاد المساحات والطرق الحسابية المثلث  ونرمز المساحة , مساحة الشكل عن طريق إمرار عدسة الرصد علي حدود الشكل وقراءة عدد الدورات من العداد ومن ثم استخدام قانون المساحة.

2-مصادر تقدير المساحة

يوجد مصدران أساسيان لتقدير المساحة وهما:

الطبيعة :

 تعتمد هذه الطريقة علي أخذ البيانات عن أطوال أو أشكال نحتاجها لتعين المسطحات , وتعتبر هذه الطريقة من أدق الطرق لعدم وجود أي أخطاء بها.

الخرائط :

 رغم أنها تحتوي في بعض الاحيان علي أخطاء ناتجة عن أخطاء الرسم لكنها تستعمل بكثرة لأنها بسيطة وسهلة.

3-طرق إيجاد المساحة

 يمكن تقسيم الطرق العامة المستخدمة لأيجاد المساحة عموما الي :

الطرق الميكانيكية:

وهي طريقة بيانية تعتمد علي استعمال أجهزة خاصة كالبلانيمتر planimeter لتعيين المساحات المختلفة وتستخدم الطرق الميكانيكية . خصوصا للأراضي ذات التعاريج  والالتواءات  وهو يتركب من الاجزاء الموضحة بالرسم أدناه.

جهاز قياس المساحة

4-قياس المساحة بجهاز البلانيميتر

 أنه يمكن الحصول علي  دقة عالية من هذه الطريقة وطريقته تتلخص فيما يلي  تؤخذ مساحة الشكل عن طريق إمرار عدسة الرصد علي حدود الشكل وقراءة عدد الدورات من العداد ومن ثم استخدام القانون وهناك حالتان عند استخدام الجهاز حيث إما يوضع الثقل داخل الشكل, أو إن لم يتسن ذلك يوضع خارجه.

قانون  الحالة الاولي حساب المساحة بجهاز البلانيميتر  : الثقل خارج الشكل

A = f ( rf - ri )
حيث أن ,
Rf - القراءة النهائية  )final reading)
Ri  -  القراءة الابتدائية )initial reading
F   -  معامل الجهاز ) instrument factor ) من الجدول المرافق للجهاز يمكن أيجاد F ياستخدام شكل معلوم للمساحة .

قانون الحالة الثانية حساب المساحة بجهاز البلانيميتر : الثقل داخل الشكل

C +  )RI  -Rf ) = A
حيث أن C  ثابت وهو يضاف بسبب أن هناك مساحة لم تقاس وهي تدعي دائرة  الصفر (zero circle) ويؤخذ من الجدول للجهاز .

5-الطرق الحسابية لمعرفة المساحة

تعتمد هذه الطريقة علي تقسيم الارض المراد مساحتها الي أشكال هندسية منتظمة كالمثلثات , المربعات , المستطيلات وغيرها بحيث يمكن حسابها باستعمال المعادلات الرياضية وتعتبر هذه الطريقة دقيقة ونسبة الاخطاء فيها ضئيلة جدا وتعتمد علي تقسيم القطعة الارضية الي أشكال هندسية  منتظمة كالمثلثات أو أشكال أخري  ثم نقوم بحساب مساحة كل شكل علي حدي وبعد ذلك نقوم بجمع كل مساحات الاشكال لنحصل علي المساحة الكلية للقطعة الارضية.

 وفيما يلي بعض المساحات باستعمال المعادلات الرياضية لاشكال منتظمة:

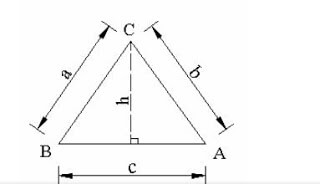
أ- قانون حساب مساحة المثلث

المثلث triangle

نرمز ب area للمساحة

_______________    =     area

  (c-s)(s-b)(s-a)s    |\

حيث أن a+ b + c

         _________   =  S

حساب المساحة بطريقة المثلث

ب- قانون حساب مساحة المربع

المربع square

a= ca= dc = bd =ab

area = a2 

مساحة المربع

ج- قانون حساب مساحة المستطيل

المستطيل  rectangle

ac = b d = a

ba= dc = b

area =a ×b

قياس مساحة المستطيل

د - قانون حساب مساحة متوازي الاضلاع

متوازي الاضلاع parallelogram

   ab=dc=b
area=b×h

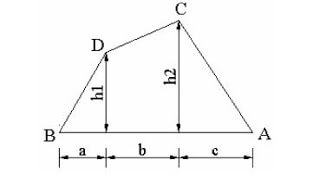
ه - قانون حساب مساحة شبه المنحرف

شبه المنحرف  trapezium

area = (h1+h2).b+a.h1+c.h2)/2

المساحة شبه المنحرف

 

 area =(h+h).b +a.h+a.h)/2=b.h+a.h

area = (m.r2.0)360

area=m.r2

المساحة

area= (2.l.r)/3

area= m. r1.r2

 area= r.l/2

   

                 
______
area = m.r.   |/ r2 + h2

area = 2. m.r.h

area = m. s. (r+r)

6- الطرق النصف حسابية

وهي خاصة عموما بحساب المساحات الضيقة حيث يمكن تقسيم الارض الي شرائح وتستعمل قوانين خاصة بها سوف نتطرق اليها فيما يلي :

أ-طريقة حساب مساحة اشباه المنحرفات trapezoidal method

يفترض في طريقة اشباه المنحرفات أن تقسم الارض المراد حساب مساحتها الي عدة أقسام متساوية المسافة المنتظمة بين بعدين عموديين بحيث أن كل قسم عبارة عن شبة منحرف له عمودان متوازيان ومسافة منتظمة بين هذين العمودين.

ب- مساحة علي شكل شبه منحرف

المسافة المنتظمة بين بعدين عموديين
يمكن حساب المساحة A c d b كالتالي:

area = l. (h1+hn/2 + h2+h3+h4+000+hn-1)

,وسوف اتناول ان شاء الله الطريقة الخاصة بالتطبيق والامثلة علي الحل: